🔑 코인 투자 추천 링크 🔑
1. 이동평균 정의(Moving Average(MA)
이동 평균 (MA)은 일정 기간 동안 유가 증권의 평균 가격을 표시하는 가격 기반의 지연 (또는 반응) 지표입니다. 이동 평균은 모멘텀을 측정하고 추세를 확인하고 지원 및 저항 영역을 정의하는 좋은 방법입니다. 본질적으로 이동 평균은 차트를 해석 할 때 "노이즈"를 부드럽게합니다. 소음은 가격과 볼륨의 변동으로 구성됩니다.
이동 평균은 지연 지표이고 이미 발생한 이벤트에 반응하기 때문에 예측 지표로 사용되지 않고 확인 및 분석에 사용되는 해석 지표로 사용됩니다. 실제로 이동 평균은 Bollinger Bands 및 MACD와 같은 여러 다른 잘 알려진 기술 분석 도구의 기초를 형성합니다. 모두 동일한 기본 전제를 취하고 변형을 추가하는 몇 가지 유형의 이동 평균이 있습니다. 가장 주목할만한 것은 단순 이동 평균 (SMA), 지수 이동 평균 (EMA) 및 가중 이동 평균 (WMA)입니다.
2. Moving Average Pine Script 소스
//@version=4
study(title="Moving Average", shorttitle="MA", overlay=true, resolution="")
len = input(9, minval=1, title="Length")
src = input(close, title="Source")
offset = input(title="Offset", type=input.integer, defval=0, minval=-500, maxval=500)
out = sma(src, len)
plot(out, color=color.blue, title="MA", offset=offset)위 Moving Average 소스의 핵심은 out = sma(src, leg) 부분입니다.
Pine Script에서 sma함수는 이동 평균값을 리턴하며, x 의 최근 y 개를 더한 값을 y 로 나눈 값을 의미합니다.
3. 4시간 기준 BTC 이동평균이동선 예시)

4. 단순이동평균(Simple Moving Average, SMA)
단순 이동 평균은 비가중 이동 평균(unweighted Moving Average)입니다. 즉, 데이터 세트의 매일의 중요성과 가중치가 동일합니다. 새로운 날이 끝날때마다 가장 오래된 데이터 포인트가 삭제되고 가장 새로운 데이터 포인트가 처음에 추가됩니다.
단순이동평균(SMA) 계산방식
Sum of Period Values(전체 기간의 값의 합) / Number of Periods (각 기간의 값)
Closing Prices to be used(종가의 값): 5, 6, 7, 8, 9
First Day of 3 Period SMA(3일중 첫째날 SMA): (5 + 6 + 7) / 3 = 6
Second Day of 3 Period SMA(3일중 둘째날 SMA): (6 + 7 + 8) / 3 = 7
Third Day of 3 Period SMA(3일중 세째날 SMA): (7 + 8 + 9) /3 = 8
5. 가중 이동 평균(Weighted Moving Average, WMA)
가중 이동 평균은 SMA와 유사하지만 WMA가 더 최근의 데이터 포인트에 중요성을 추가한다는 점이 다릅니다. 기간 내의 각 포인트에는 해당 특정 데이터 포인트의 가중치 또는 중요도를 변경하는 승수 (최신 데이터 포인트에 대한 가장 큰 승수 및 순서대로 내림)가 할당됩니다. 그런 다음 SMA와 마찬가지로 새 데이터 포인트가 처음에 추가되면 가장 오래된 데이터 포인트가 버려집니다.
가중이동평균(WMA) 계산방식
각 기간에 가중치 (승수)를 추가한다는 점을 제외하면 SMA와 유사합니다. 가장 최근 기간이 가장 가중치가 있습니다.
5주기 WMA의 예
Sum of Period Values / Number of Periods
Closing Prices to be used: 5, 6, 7, 8, 9
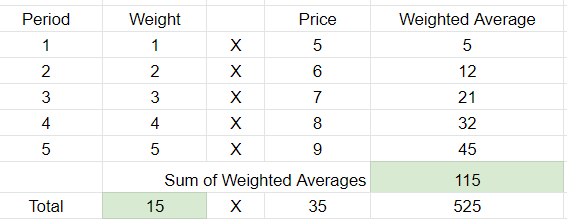
WMA = (Sum of Weighted Averages) / (Sum of Weight)
평균 가중치의 합 / 가중치의 합
WMA 115 / 15 = 7.6667
6. 지수 이동 평균(Exponential Moving Average, EMA)
지수 이동 평균은 WMA와 매우 유사하며 일종의 WMA입니다. EMA와의 주요 차이점은 오래된 데이터 포인트가 평균을 벗어나지 않는다는 것입니다. 명확히하기 위해, 이전 데이터 포인트는 선택한 데이터 시리즈 길이를 벗어나더라도 승수를 유지합니다 (거의 아무것도 감소하지 않음).
지수이동평균(EMA) 계산방식
1. SMA를 먼저 계산합니다. (기간의 값 / 기간의 숫자)
2. 승수(Multiplier)를 구합니다.
2 / (기간의 숫자 + 1)
즉, 2 / (5+1) = 33. 333% 가 됩니다.
3. EMA를 계산합니다 .
- EMA 첫째날을 구하기 위해서 EMA(이전날) 대신에 SMA(이전날)을 사용합니다.
EMA = {Close - EMA(previous day)} x multiplier + EMA(previous day)
Double Exponential Moving Average
EMA = 2*EMA – EMA (EMA)
Triple Exponential Moving Average
EMA = (3*EMA – 3*EMA(EMA)) + EMA(EMA(EMA))




댓글